Recently, I was watching Harry Potter and the Deathly Hallows, part 1. The score was written by Alexandre Desplat. In this movie, there is a (quite beautiful) scene where Harry opens a Horcrux (the locket) in order for Ron to destroy it. As he does, apparitions come out of the locket, torturing Ron by playing with his fears. Here is the soundtrack which happens in the movie at that moment:
When I first saw that scene and listened to the music, I was struck by the chords which occur between 24” and 32”. It reminded me of something, but I couldn’t figure out what.
And then I remembered: there was something very similar in a piece by Bernard Herrmann, who composed the music of many movies for Alfred Hitchcock. More specifically, I was thinking about the prelude of Fahrenheit 451 (which is a Truffaut movie, by the way). Here it is:
I had been introduced to the music of Herrmann more than 15 years ago, and when I was younger, I wanted to understand how it had been composed, without any success however. With a little experience in transformational music analysis, it appears much simpler now.
The prelude opens with a D major chord in the first half of bar 1, and then switches to a Bb minor chord for the remaining half. This is then repeated on bar 2. Here are the chords in a graphical way:

Observe that the transition from one chord to the other is quite parsimonious, as it involves only movements by semitones. And here are the chords in the neo-Riemannian tonnetz:
So, immediately, we can see that the LPL transformation connects the D major chord to the Bb minor chord.
Then, on bar 3 (9”), the chords change. We have first a F# major chord for the first half, and then a D minor chord. Here they are:
And in the Tonnetz:
And we see that going from F# major to D minor involves…. the LPL transformation.
Ah ha ! Quite symmetric, isn’t it ?
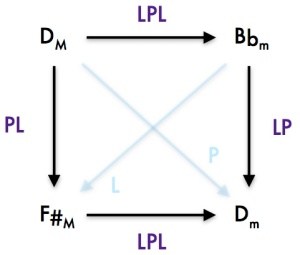
Now, given that the elements of the T/I group commute with the elements of the PLR group, we can arrange the four chords in the following diagram:

But we would be missing one important detail. Let’s look at all four chords in a graphical way:
We can clearly see the symmetry between chords by the transformation. But we can also observe that all these chords share a number of common pitch classes, which suggest that neo-Riemannian transformations could play an important role here as well. Indeed, if we represent everything in the Tonnetz, we will observe a very symmetric disposition (the lighter red dots are the repeated images of the chords, because, as you surely remember, the Tonnetz is topologically a torus):
The transformations between these chords can then be described by the following diagram:
Given that PL is the inverse of LP, we have here an even more symmetric description of the chords than with the transformation.
And what is the relation with the locket of Harry Potter ? Well, at 24” in the above soundtrack, we hear a D major chord, while the melody starts on a E, then goes down to D, then C#. As it goes down to Bb, the harmony changes to a Bb minor chord. The melody then jumps one octave up on Bb, and then resolve on A as the harmony changes back to a D major chord.
Thus the resolution is also described by a LPL transformation (LPL is its own inverse), with the same chords as in the music of the prelude of Fahrenheit 451, except in a reversed order. As on previous occasions, I may have noticed a “neo-riemanny” taste in these two scores….





What program did you make the pc circle diagrams with? I’m writing a paper using them & wonder if there’s a nice easy graphic solution to displaying them. Thanks.
Nothing automatic, I use Apple Keynote for those diagrams…
Interesting – I’m a huge fan of Herrmann’s work but have never taken the time to really understand his techniques. Very useful – Thanks!
I really enjoy the way you connect the maths with actual musical examples via the tonnetz in these examples, please keep going!